
24H全国咨询热线

微信


免费通话

Language
新闻中心
News Center
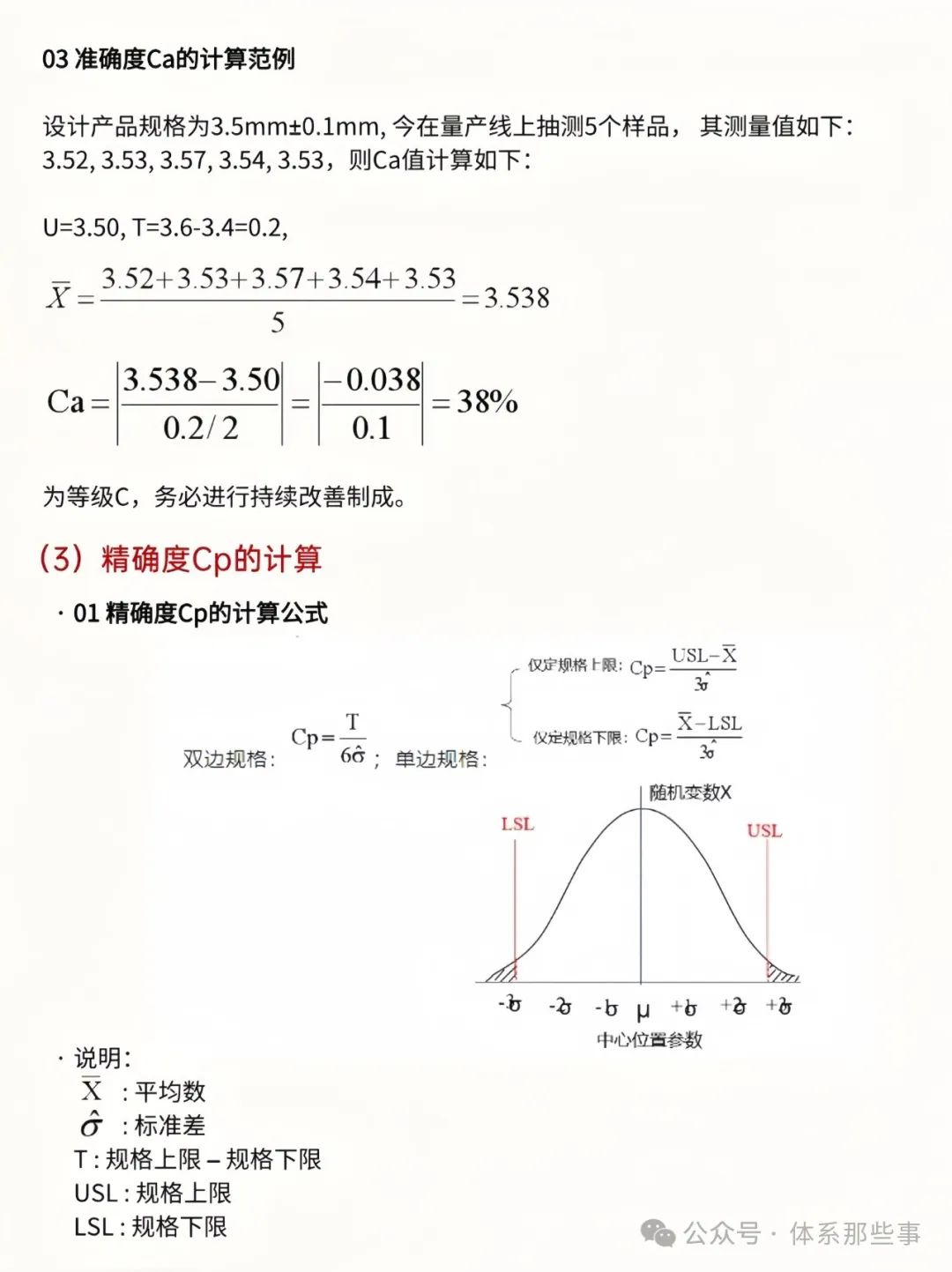
产品批量生产中的质量控制:Cpk大于1.33的重要性解析
Jul 18,2025
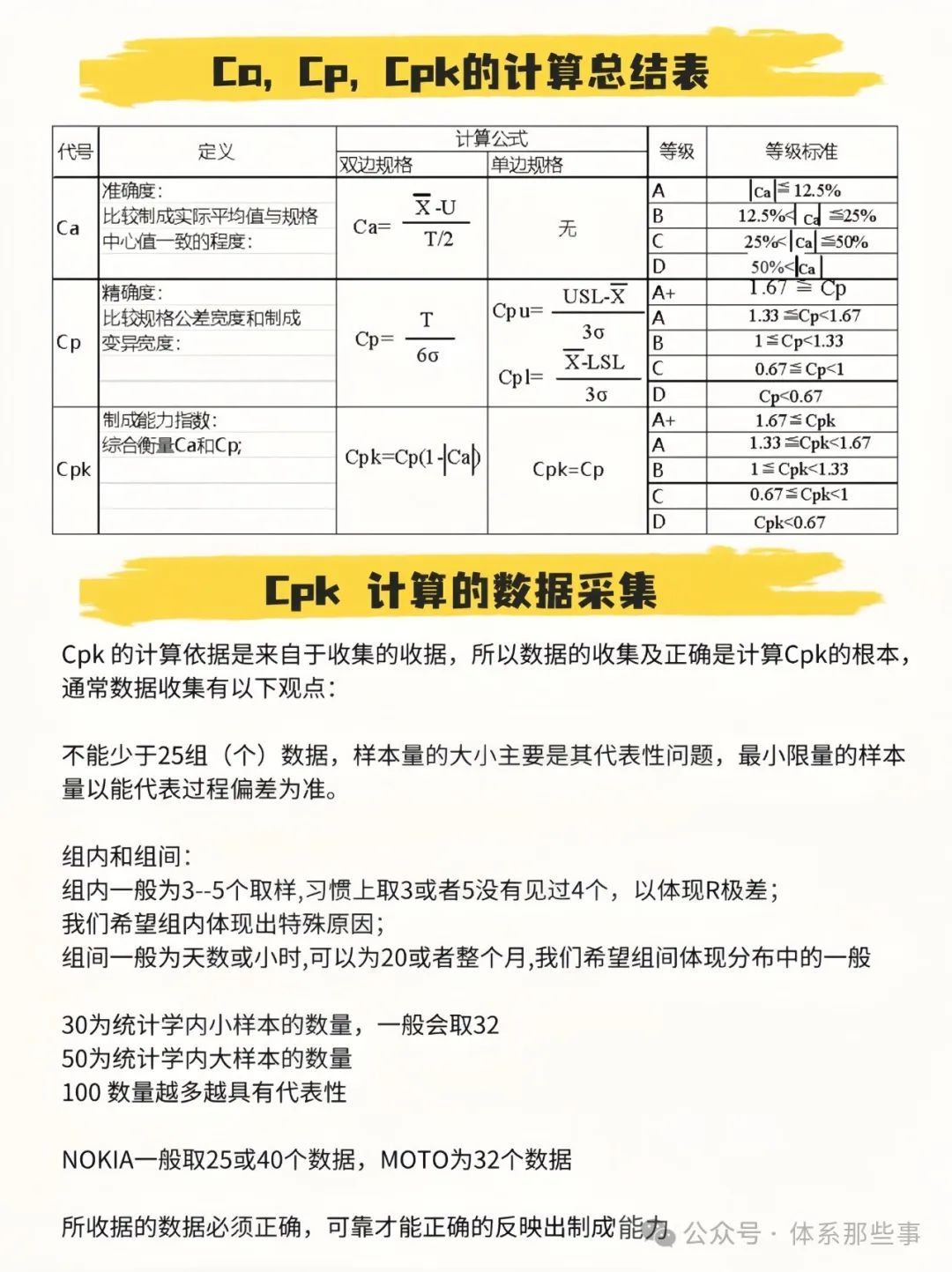
Cpk过程能力指数是指过程能力满足产品质量标准要求(规格范围等)的程度。也称工序能力指数,是指工序在一定时间里,处于控制状态(稳定状态)下的实际加工能力。它是工序固有的能力,或者说它是工序保证质量的能力。它是每个质量人必备技能,它是衡量生产过程能力高低的数据,对质量管理、质量提升非常重要。
前言
Cpk=1.33这一数值背后究竟隐藏着怎样的意义?
为何只有当Cpk大于1.33时,才适宜进行批量生产?
达到此标准后,产品的良品率与不良品率又会如何分布?
从字面上看,Cpk>1.33似乎难以直观理解其深层含义。
但如果我们换一种方式表达,即在一百万个零件中,仅有63个是不良品,这样的表述是否就更加清晰了呢?这样的数据如何得出?难道真的是逐个零件进行检测吗?显然,这并不现实。那么,有没有其他方法可以更高效地得出这一结论呢?
全检与抽检
在生产过程中,每个零件都有两种可能:合格或不合格。如何判断一个零件是否达标呢?这里有两种常用的方法:全检和抽检。
方法一:全检
全检,顾名思义,就是对每一个零件都进行详细的检测。如果零件满足预设的检验标准,那么它就被判定为合格品;否则,就被视为不合格。然而,全检虽然直观可靠,但它耗时耗力,成本相对较高。因此,它更适合于小批量生产、质量不稳定或要求特别高的情况。
方法二:抽检
与全检不同,抽检是从一批零件中随机抽取一定数量的样本进行检测。根据这些样本的检测结果,我们可以推断整批零件的质量状况。抽检的优点在于节省时间、人力和成本,因此更适用于大批量生产、质量稳定或要求不那么严格的情况。但需要注意的是,抽检存在一定风险,因为即使抽检结果显示合格,也不能完全排除整批零件中可能存在的不合格品。为了确保产品质量,我们需要在数学工具的辅助下对不良率进行量化评估,并努力将其控制在可接受的范围内。
那么,如何计算抽检中的不良率呢?当我们面对一个零件的某个尺寸呈正态分布的情况时,应该如何进行不良率的计算呢?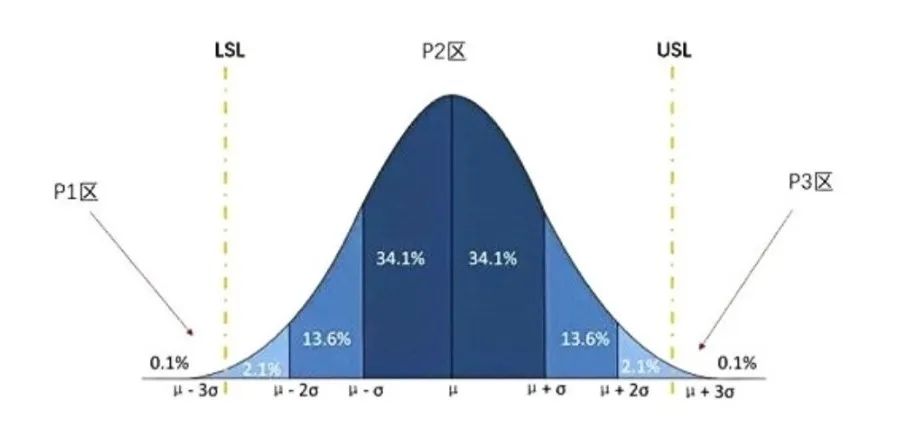
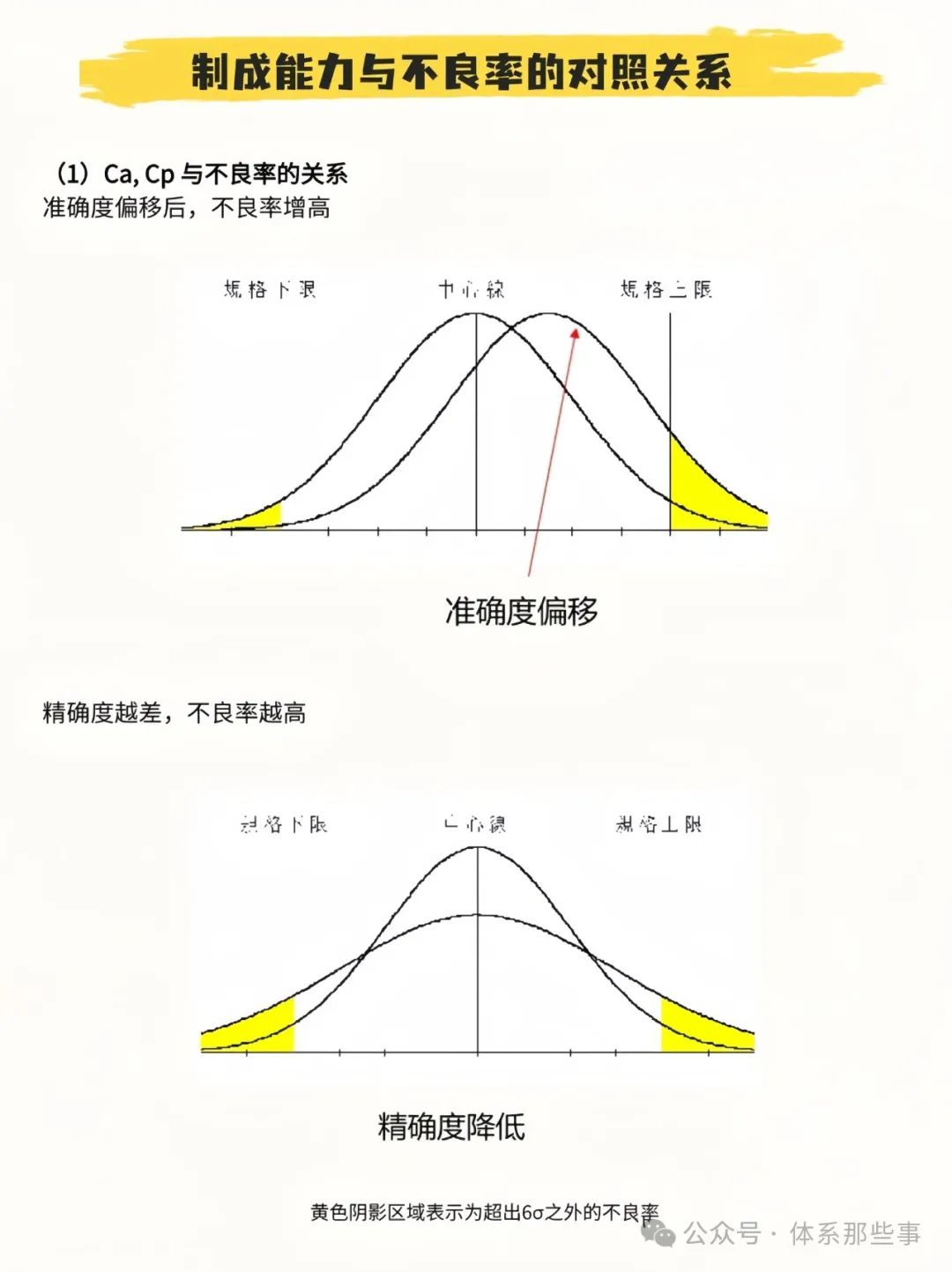
由上图,我们可以清晰地看到,不良率是由超过上规格线USL和下规格线LSL的面积总和来计算的。换句话说,不良率等于超过USL部分的面积P1与超过LSL部分的面积P3之和。
为了更精确地计算这些面积,我们可以利用正态分布的面积函数,即标准正态分布函数F(x)。这个函数能够根据输入值x,快速给出(-∞,x)范围内的面积,也就是我们所需的概率面积。

计算完成后,我们揭示了Cpk与不良率(以PPM表示)之间的关联:
PPM = 1000000 * [2 - 2F(3Cpk)]
同时,良品率则可以通过1减去不良率来得到,即:
良品率 = 1 - PPM = 2F(3Cpk) - 1
值得注意的是,在过程输出的均值发生漂移的情况下,Cpk不再等于Cp,此时建议采用积分函数来进行更为精确的计算。
在计算过程中,我们需要查阅标准正态分布函数F(x)的相关附表。在μ=0,σ=1的条件下,所遵循的正态分布被定义为标准正态分布。例如,当x=3,即Cpk=1时,我们可以利用计算器(如下图所示)来求得F(x)的值为0.998650,进而得出F(3Cpk)=0.998650的结果。
因此,可以计算出PPM(百万分之一缺陷率)为:
PPM = 1000000 * [2 - 2F(3Cpk)] = 2700,
同时,良品率P可以通过以下公式得出:
良品率 = 1 - P = 2F(3Cpk) - 1 = 0.9973。
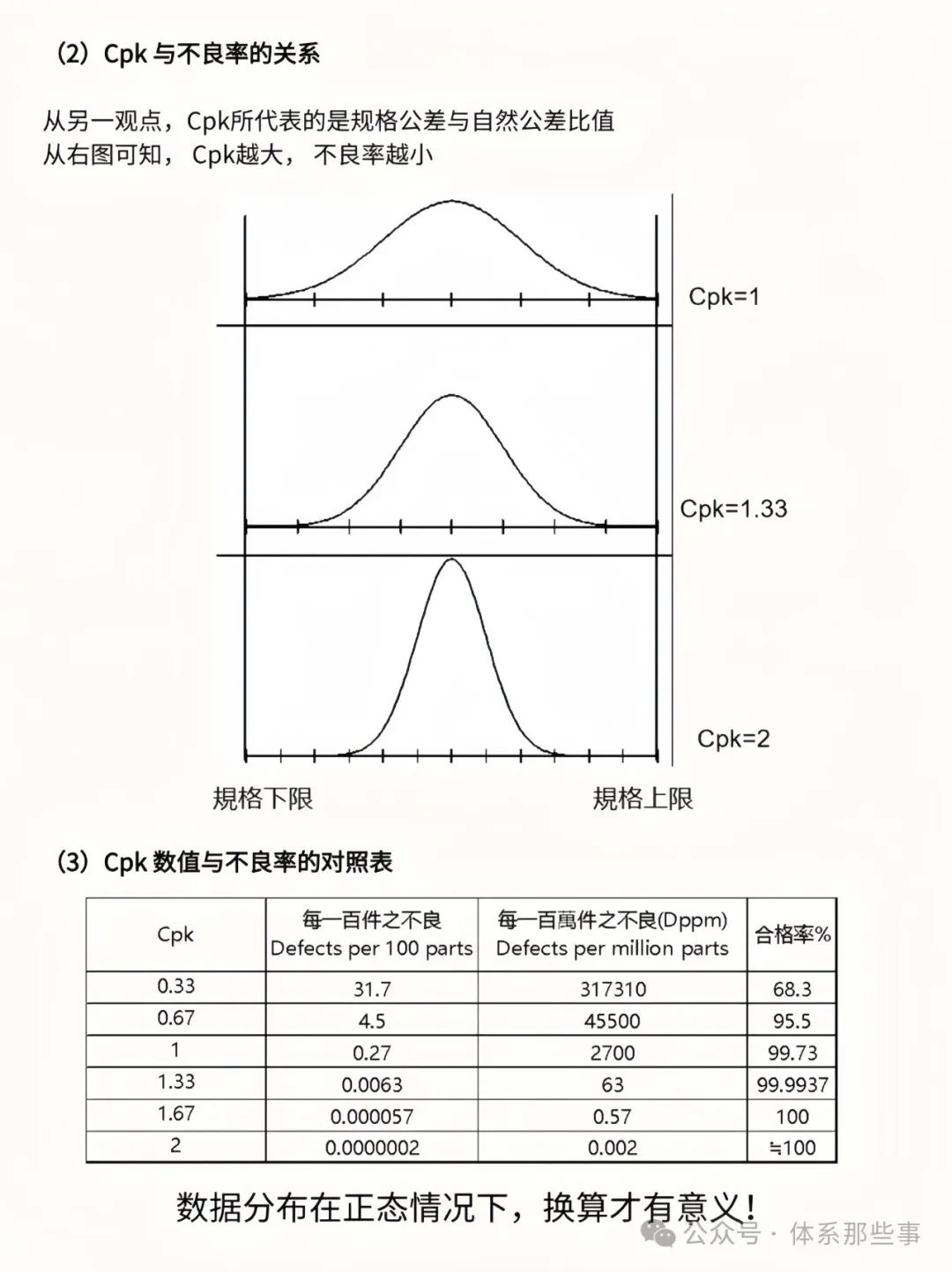
当Cpk取不同的值时,相应的不良率PPM和良品率P的值如下表所示:
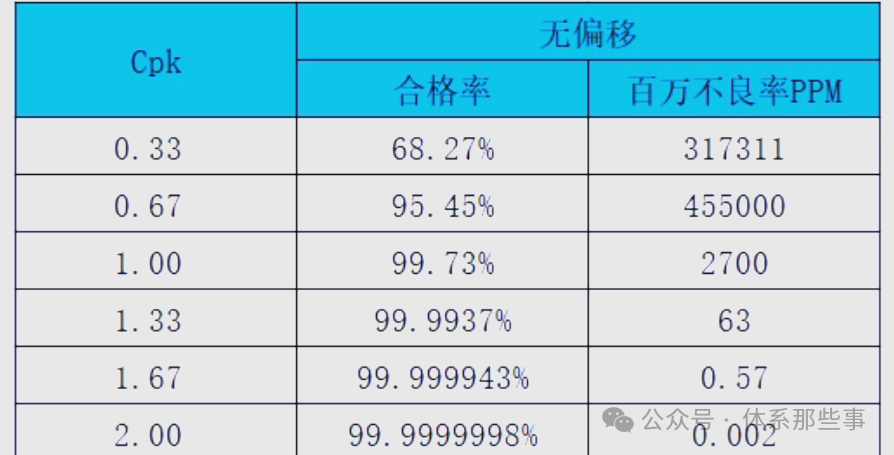
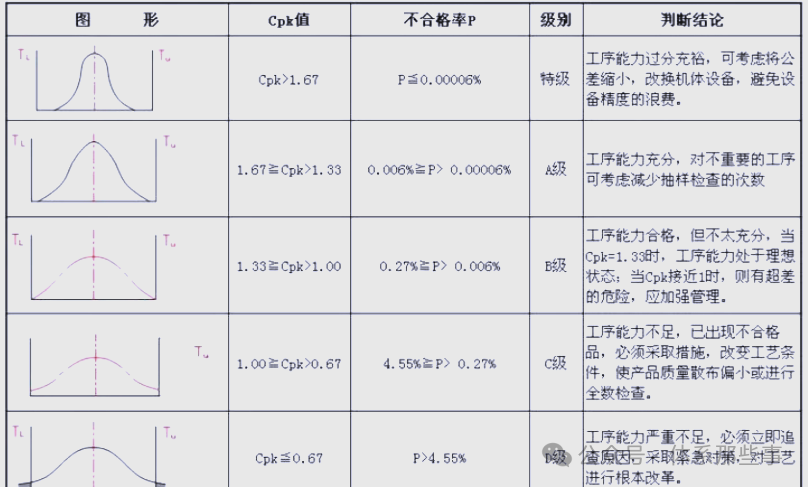
通过全检方式,人工剔除不良品能直接得出不良率,但面对大批量生产时,这种方式成本高昂。若采用抽检,虽能计算批次不良率,但计算过程相对繁琐。在实际操作中,我们通常采用Cpk来衡量,它反映了持续生产良品的过程制造能力。低过程能力往往伴随着较高的不良率和多不良品产出,而高过程能力则意味着低不良率。根据Cpk的不同值,我们可以判断制程能力的强弱。通常,只有当Cpk达到1.33及以上时,才适合进行批量生产。
03
为什么Cpk>1.33才能量产
那么,为什么只有当Cpk达到1.33及以上时才适宜进行批量生产呢?
这个标准是如何来的呢?
我们可以通过推导PPM公式来解答这个问题。
PPM公式为:
PPM=1000000*[2-2F(3Cpk)],
其中F(3Cpk)实际上代表了西格玛水平=3Cpk(σ),这是在无偏移情况下的对应关系。通过这个公式和推导过程,我们可以理解为何Cpk达到1.33是批量生产的适宜标准。
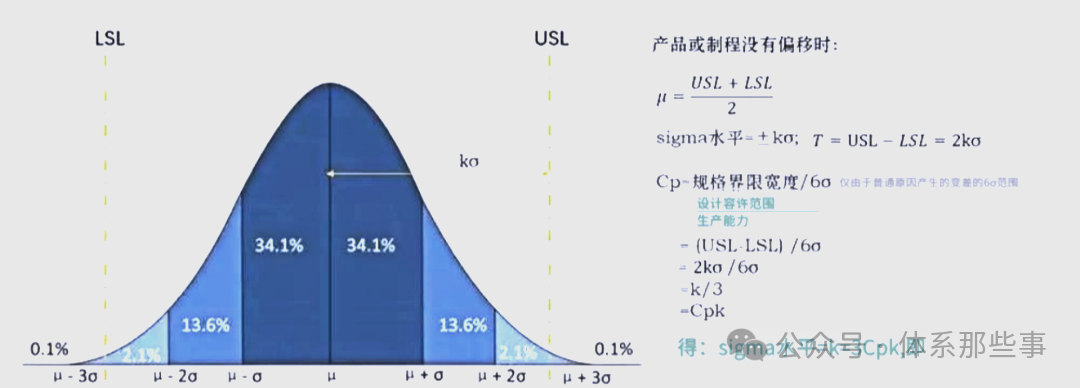
当Cpk达到1.33时,其对应的西格玛水平为3乘以1.33,即3.99σ,这大约等于4σ。这意味着,当Cpk值为1.33时,产品的品质已经具备了4σ的能力。
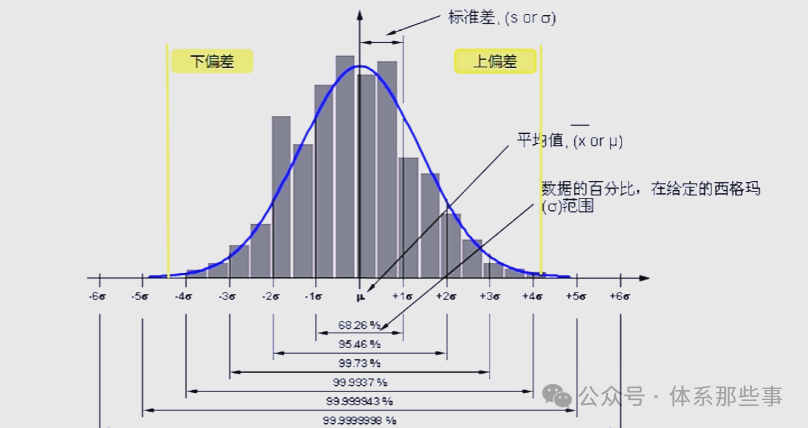
下图展示了不同的Cpk值所对应的西格玛水平以及PPM(百万分之一)的值。
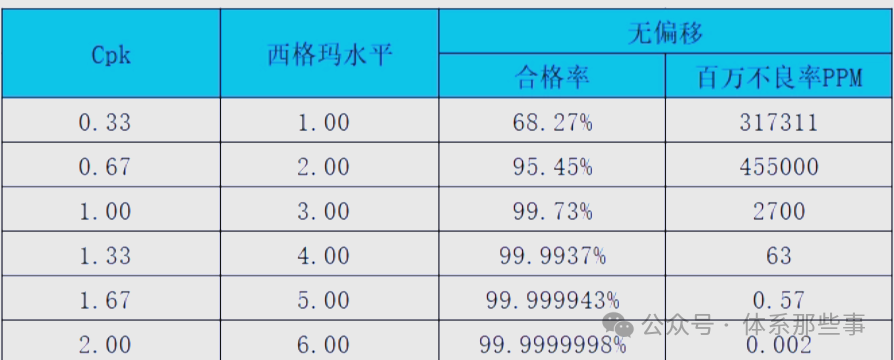
西格玛&西格玛水平
这里需要澄清两个概念:西格玛与西格玛水平。
西格玛,即标准偏差。
是衡量一组数据偏离均值程度的统计量,以希腊字符σ表示。
而西格玛水平,则是将过程输出的平均值、标准差与质量要求的目标值、规格限进行对比,从而衡量过程满足质量要求的能力。西格玛水平越高,该过程满足质量要求的能力就越强,相应的质量水平也就越高;反之则越低。
那么,为什么行业内普遍认为Cpk必须达到1.33以上才适合进行批量生产呢?这主要源于对质量和成本的权衡。
当企业的生产水平达到约4个西格玛时,虽然不能完全避免不良品的出现,但通过全检来发现并剔除这些不良品的成本变得相对较高。因此,结合成本和质量的需求,行业内形成了Cpk=1.33这一标准。
通常,只有当Cpk达到或超过1.33时,企业才会考虑进行批量生产,以确保在质量和成本之间达到最优的平衡。







*本资料部分信息源于公开网络渠道,其版权归属原作者所有。
若内容涉及版权争议或授权问题,请通过halllaser@halllaser.com 联系我司,我们将依法配合处理。
上一页:
下一页:













